Breadth First Search (BFS) is a graph traversal algorithm that explores nodes in order of their distance from a starting point. BFS guarantees the shortest path between two nodes in an unweighted graph, making it essential for navigation systems, social network analysis, network routing, and puzzle-solving.
The algorithm works by visiting all nodes at distance 1 from the source before examining any nodes at distance 2, then all nodes at distance 2 before examining distance 3, and so on. This systematic exploration uses a queue data structure and a visited set to maintain correctness.
Most developers can implement BFS in minutes. Queue, visited set, level-by-level processing. Code compiles, tests pass. But understanding why BFS guarantees shortest paths differs from knowing how to implement it. That distinction determines whether you can identify when AI-generated code applies BFS incorrectly to weighted graphs, where it counts hops instead of edge weights and produces wrong answers.
This guide covers BFS from correctness guarantees through practical applications and common failure modes, starting with mechanisms before patterns.
The correctness guarantee explained
BFS maintains one fundamental rule: when you visit a node for the first time, you've reached it via the shortest possible path from the source.
This is because BFS explores nodes in strict distance order. It processes all nodes at distance 1 before examining any at distance 2. All at distance 2 before any at distance 3. When BFS first encounters a node, no shorter path can exist. Any shorter path would have discovered that node earlier.
The queue creates this ordering. When you enqueue a node's neighbors, you're adding nodes exactly one edge farther from the source. FIFO behavior ensures you finish all nodes at distance d before starting on distance d+1.
The visited set prevents re-examining nodes you've already reached via the shortest path. Once visited, you've found its shortest distance. Re-exploring wastes time without improving results.
This guarantee only holds for unweighted graphs or graphs where all edges have identical weight. The moment edge weights vary, BFS's distance ordering breaks. It processes nodes by hop count, not actual distance.
When BFS guarantees break down
The shortest-path guarantee only holds for unweighted graphs. In weighted graphs, BFS gives you the path with the fewest edges, not minimum total weight.
Take three nodes: A, B, and C. There's a direct edge from A to C with weight 100, and edges A→B and B→C, each with weight 1. BFS chooses the direct path A→C (fewer edges) even though A→B→C has lower total cost (2 vs. 100).
For weighted graphs, use Dijkstra's algorithm (non-negative weights) or Bellman-Ford (negative weights). BFS optimizes for hop count, not cumulative cost.
The guarantee also fails if your graph representation is incorrect. If adjacency lists don't include all edges, or neighbor generation has bugs in implicit graphs, BFS still runs. But it finds shortest paths only within the graph structure you provided, not the one you intended.
How does Breadth First Search work?
BFS creates its correctness guarantee through three interconnected mechanisms.
The queue maintains FIFO ordering. When you dequeue a node, you process it in discovery order. When you enqueue its neighbors, you schedule them after all nodes at the same distance. A source node with three neighbors a, b, c gets processed first. You enqueue a, b, c. The queue ensures you process all three before processing any of their neighbors.
Compare this to Depth First Search, which uses a stack. DFS explores as far as possible along one branch before backtracking. That's useful for topological sorting and cycle detection, but it doesn't maintain distance ordering and can't guarantee shortest paths.
The visited set serves three purposes. It prevents infinite loops in graphs with cycles. It prevents exponential blowup when the same node is reachable through multiple paths. And it enforces the "shortest path first" property. Once you've visited a node, you've found the shortest distance to reach it. Processing it again can't improve that result.
The order of operations determines correctness. Mark the starting node as visited and enqueue it. While the queue isn't empty, dequeue a node, then for each unvisited neighbor, mark it visited, enqueue it, and record any metadata.
You mark neighbors as visited when you enqueue them, not when you dequeue them. Otherwise a node with multiple incoming edges gets enqueued once for each parent, creating massive inefficiency in dense graphs.
Graph representations affect performance
An adjacency list stores each node's neighbors in a dictionary. Space complexity is O(V + E). For BFS, adjacency lists are usually optimal since you iterate through all neighbors anyway.
An adjacency matrix uses O(V²) space regardless of edge count. Wasteful for sparse graphs but acceptable for dense graphs where E approaches V². Checking if an edge exists is O(1).
An edge list is memory-efficient at O(E) space but inefficient for BFS. Finding a node's neighbors requires scanning the entire list.
Implicit graphs generate neighbors on the fly. In a maze, each cell's neighbors are adjacent cells that aren't walls. In word ladder problems, each word's neighbors are valid words differing by one letter. BFS remains unchanged. You just call generate_neighbors(current) instead of looking up graph[current].
Basic implementation
The simplest BFS determines reachability:
from collections import deque
def bfs_reachable(graph, start):
visited = {start}
queue = deque([start])
while queue:
current = queue.popleft()
for neighbor in graph[current]:
if neighbor not in visited:
visited.add(neighbor)
queue.append(neighbor)
return visitedFor shortest paths, track predecessors:
def bfs_shortest_path(graph, start, target):
if start == target:
return [start]
visited = {start}
queue = deque([start])
predecessors = {start: None}
while queue:
current = queue.popleft()
for neighbor in graph[current]:
if neighbor not in visited:
visited.add(neighbor)
queue.append(neighbor)
predecessors[neighbor] = current
if neighbor == target:
# Reconstruct path
path = []
node = target
while node:
path.append(node)
node = predecessors[node]
return path[::-1]
return NoneThe early termination matters. As soon as you discover the target when enqueueing it, return. BFS guarantees you've found the shortest path.
Complexity analysis
BFS runs in O(V + E) time. It visits each vertex once and examines each edge once. The V term accounts for vertex processing. The E term accounts for iterating through adjacency lists.
Use collections.deque for O(1) enqueue and dequeue. If you use a list and pop from the front with list.pop(0), you get O(V) per dequeue due to element shifting, making overall complexity O(V²).
Space complexity is O(V) in the worst case. The queue might contain all nodes at a given distance level. For a very wide graph in which each node connects to all others, the queue could hold V-1 nodes simultaneously.
Real-world applications of BFS
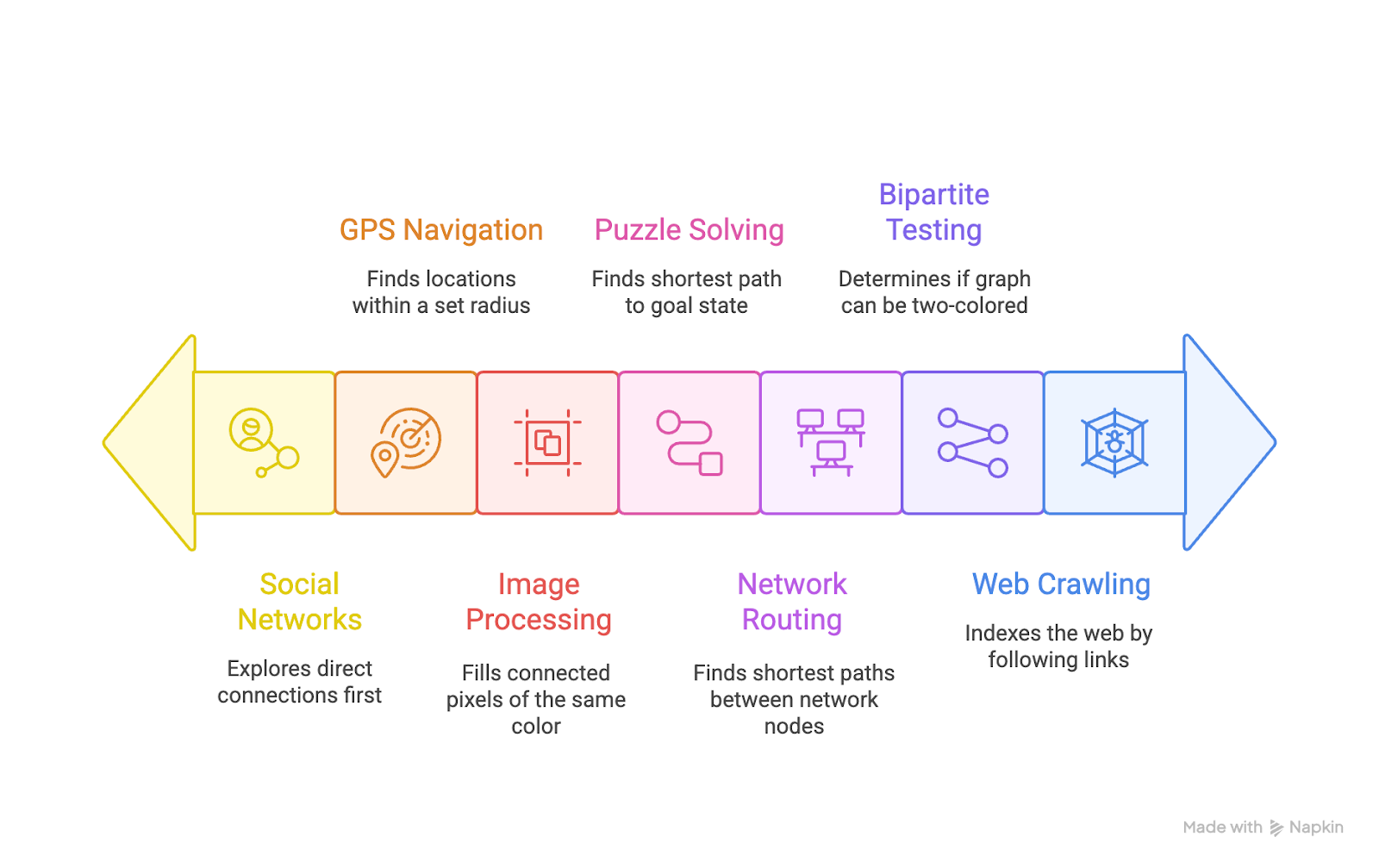
BFS's correctness guarantee explains why it appears across so many domains. Any problem requiring shortest paths in unweighted graphs, level-based processing, or systematic exploration benefits from BFS.
- Network routing: RIP (Routing Information Protocol) uses hop count as its metric. When a router needs to find the best path to another network, it counts the number of routers (hops) between the source and destination. BFS finds minimum-hop routes between network nodes, making it ideal for protocols where each hop has equal cost.
- Social networks: Finding degrees of separation ("six degrees of Kevin Bacon"), identifying users within k hops of a given person, or discovering potential connections all use BFS. The algorithm explores your immediate connections first, then friends-of-friends, then friends-of-friends-of-friends, exactly matching how social distance works.
- Puzzle solving: Sliding tile puzzles, robot navigation, and word ladders model states as nodes and valid moves as edges. Each state's neighbors are reachable in one move. BFS finds the minimum number of moves to reach the goal state because it explores all states reachable in n moves before examining any states requiring n+1 moves.
- GPS navigation: "Show me all restaurants within 2 miles" translates to "give me all nodes within distance d in a graph where edges represent roads." BFS naturally groups locations by distance from your starting point, processing all locations at 1 mile before examining locations at 2 miles.
- Image processing: Flood fill explores all pixels of the same color reachable from a starting pixel. Click a region in an image editor, and BFS finds all connected pixels of that color. The same mechanism handles connected component labeling in image segmentation, which involves identifying distinct regions in an image.
- Web crawling: Search engines use BFS-based crawling to index the web. Starting from known seed URLs, crawlers follow links breadth-first. This prioritizes quickly discovering new pages over fully exploring any single site. If you used DFS instead, you'd dive deep into one website's link structure before finding any pages on other sites, creating a stale index.
- Bipartite testing: A graph is bipartite if you can color its nodes with two colors such that no edge connects the same-colored nodes. Start BFS from any node and assign it color 0. For each neighbor, assign the opposite color (1). Continue BFS, alternating colors as you explore. If you try to assign a node a different color than it already has, the graph isn't bipartite. This determines whether matching problems (jobs to workers, students to projects, tasks to processors) have valid solutions.
When to use BFS
BFS isn't always the right choice. The decision depends on what you're trying to accomplish and the constraints of your graph. Here is when you need to use BFS:
- Shortest paths in unweighted graphs: If all edges have equal cost and you need the minimum number of hops, BFS gives you the answer efficiently.
- Level-order traversal: When you need to process nodes by their distance from a starting point (for example, finding all nodes within k hops of a source), BFS naturally provides this grouping.
- Finding connected components: a BFS starting from each unvisited node identifies all nodes reachable from that node, partitioning the graph into connected components.
- Guaranteed completeness: BFS will find a solution if one exists. For problems where you need to explore all possibilities at a given distance before moving farther, BFS ensures nothing is missed.
Why understanding algorithms matters for AI training work
The difference between knowing how to implement BFS and understanding why it produces correct results is the same difference between following instructions and exercising judgment.
Training frontier AI systems requires constantly evaluating code, comparing solutions, and assessing whether generated outputs are correct. That requires understanding not just what makes code work, but what makes it correct for the problem constraints.
A developer who only memorized BFS implementation might accept AI-generated code that uses BFS for a weighted shortest-path problem. It would compile, run, and produce output. But it would give wrong answers because BFS doesn't account for edge weights.
A developer who understands BFS's correctness guarantee would catch this immediately. They'd recognize that the problem requirements conflict with BFS's assumptions and flag the solution as incorrect, even though it superficially works.
This is the kind of judgment required in AI training work. It involves evaluating whether the solution approach is correct for the problem structure, whether edge cases are handled properly, and whether the algorithm's assumptions match the problem constraints.
Contributing to frontier AI development at DataAnnotation
Can you tell when an algorithm is correct versus when it just compiles? Do you understand why BFS fails on weighted graphs, not just that it does? Can you distinguish implementations that handle edge cases from those that pass basic tests?
If your background includes the ability to evaluate algorithmic correctness, distinguish plausible code from correct code, or assess whether implementations match their problem constraints, AI training at DataAnnotation positions you at the frontier of AGI development.
If you want in, getting from interested to earning takes five straightforward steps.
- Visit the DataAnnotation application page and click "Apply"
- Complete the brief form with your background and technical expertise
- Take the Coding Starter Assessment (approximately 1-2 hours)
- Watch for the approval decision, typically within a few days
- Log into your dashboard, select projects matching your skills, and begin contributing
No signup fees. DataAnnotation stays selective to maintain quality standards. You can only take the Starter Assessment once, so read the instructions carefully and review before submitting.
Apply to DataAnnotation if you understand why algorithmic correctness matters for AI development and you have the technical judgment to evaluate it.



